Apr
10
Resolving a Cosmological Crisis
Have you heard about the “crisis” in cosmology?
“Crisis” seems a bit alarmist to me, but that’s the term some are using. It comes down to the fact that cosmologists can’t figure out how to reconcile the most recent measurements for the age of the universe. See, there are two major methodologies to deriving it, and they need to jibe (within error bars, of course) to make sure we have an accurate estimate. I’ll do my best to give you the short version of those methods and the “tension”-inducing problem.
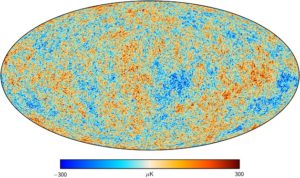
Measuring the age of the universe requires knowing the rate of expansion at different times. When you apply Einstein’s theory of general relativity to the universe, you get the Friedmann equations. These in turn allow you to “connect the contents of the universe at any one time” (e.g., dark matter, radiation, etc.) “to the expansion rate at that time.” Calculating the expansion rates at different periods of cosmic history leads to a measurement for the age of the cosmos as a whole.
The best way to measure the cosmic stuff is via the cosmic microwave background radiation (CMBR), which dates to when the universe was only ~380,000 years old. We have great CMB maps these days, but they can’t show dark energy. For that, we use other observations. As astrophysicist Paul Sutter sums up, “[O]nce you do that, you can plug everything into the Friedmann equations and get the expansion rate at any point in time (including today) and, from there, determine the age of the universe.”
Another method of going about this is to measure the Hubble constant — i.e., the present-day expansion rate of the universe — more directly. This requires measuring the distances and speeds of several astronomical objects. Perhaps the best known candidate is Type Ia supernovas. These phenomena act basically the same way whenever and wherever, always peaking at the same level of brightness, so they function as “standard candles.” Comparing peak brightness with “current” brightness leads to an estimation of the Hubble constant at the time of the supernova. (F.y.i., this was the same method used to discover dark energy in the late-1990s.)
As these methods and their instruments have improved over the past couple decades, both have gotten more precise measurements. Unfortunately, there is no overlap of error bars for the age calculations, and the two methods are separated by roughly 10-20 million years. In astronomical terms, that may not sound like much, but it is significant enough that it has astrophysicists and especially cosmologists quite puzzled.
“What’s at stake here is our modern understanding of the history of the universe, as encapsulated by the so-called Lambda-CDM model, often abbreviated as LCDM. This model makes a few base assumptions, just like any other model in science. The model assumes that general relativity is correct at cosmological scales and that our universe is homogenous and isotropic (the same in all directions). It assumes that our universe is geometrically flat and that there is some entity, called dark matter, that doesn’t often interact with normal matter (that’s the “CDM” part, for “cold dark matter”). And it assumes that there’s another substance, called dark energy (that’s the “Lambda”), that maintains a constant density as the universe expands.”
So, what could be the problem?
Given recent developments, a few scientists think we should start questioning the LCDM model itself. (Of course, most of them didn’t like it to begin with.) But, the majority are very reluctant to do so, because it “is wildly successful in describing and predicting a host of cosmological observations”. Similarly, our CMB measurements are “some of the most precise measurements ever taken in science”, and they have proven themselves time and time again in various tests and checks. What about dark energy? Well, it is quite mysterious, and many postulate that we are still missing some relevant fact(s) about it. Another possibility is that there is something about the complicated physics of supernovas that is insufficiently understood and is causing our measurements to be slightly off. (Sutter leans toward this explanation.)
Now, I would like to jump back to where I discussed the two methods for measuring the age of the universe and add the following from Sutter (and more precise measurements from Hugh Ross):
“Measurements of the early universe give us loads of information about the free parameters of the LCDM model. Those measurements come from not only the CMB but also from so-called baryon acoustic oscillations [BAO] — subtle shifts in galaxy positions left over from when giant sound waves crashed around in the early universe — and the abundance of light elements.
No matter what combination of early-universe measurements you make to fill in the LCDM model, you end up predicting a value of the Hubble constant somewhere around 68 km/s/Mpc. [The CMBR-based cosmic expansion rate is 67.4 +/- 0.5 kilometers/second/megaparsec; the BAO-based rate is 68.18 +/- 0.79 kilometers/second/megaparsec.] …

You can also try to directly measure the Hubble constant. To do this, you need to measure the distances and speeds of a bunch of objects. There are lots of options, including Type Ia supernovas, galaxy properties, Mira variables and certain kinds of red giant stars.
With the exception of the red-giant method, all of the local measurements of the Hubble constant reveal a much higher number — more like 74 km/s/Mpc. [The supernova-based rate is 74.03 +/- 1.42 kilometers/second/megaparsec.]
Interestingly or frustratingly, the red-giant method gives a number right in the middle of the two extremes — hence, the crisis.”
What is interesting to me is that astrophysicist and apologist Hugh Ross sees something worth following up on with that red-giant method, whereas Sutter seemingly ignores it. The supernova-based expansion rate mentioned above comes from the team led by Nobel laureate Adam Riess which used Cepheid variable stars to calibrate the distances to local galaxies hosting Type Ia supernovas. If I am reading it correctly, the “red-giant method” is the one used by another team of astronomers mentioned by Ross and led by Wendy Freedman, and they used tip of the red giant branch (TRGB) stars to measure distances to the supernovas. Their value for the Hubble constant is 69.8 +/- 0.8 kilometers/second/megaparsec. Freedman’s team also argued that any systematic effects — i.e., due to instrumental issues and/or physical properties of the relevant astronomical objects — would have less of an impact on their method than on the Cepheid-based method.
Taking this and other factors into consideration (e.g., the abovementioned BAO measurement and the recently discovered local matter underdensity), Ross points out that the remaining difference could indeed be statistical, most if not all of which could be resolved with higher precision measurements.

Ross then considers potential adjustments to cosmic parameters that might also resolve some of the residual tension. For example, if the dark energy equation of state varies slightly as the universe ages, the Hubble constant tension goes away. Answers to that question may soon be forthcoming. Recent and ongoing “observations of binary neutron star merger events will yield accurate, assumption-free measurements of the cosmic expansion rate at look-back times ranging from the present to at least 12 billion years ago.”
Ross ends his article with the following:
“Three additional cosmic parameter adjustments would successfully resolve the Hubble constant tension. The first would be a slightly earlier time than 375,000 years after the cosmic creation event for the universe to cool sufficiently for hydrogen atoms to form. A second adjustment would be for the curvature of the universe to depart very slightly from a flat geometry. A third adjustment would be a slightly different bound on neutrino masses. All of these adjustments can be tested for their possible validity by more accurate CMBR maps, observations of more binary neutron star merging events, and more extensive and accurate BAO and TRGB measurements.
The latest cosmological observations and proposed cosmic parameter adjustments provide multiple independent ways the Hubble constant tension can be eliminated. The biblically predicted big bang creation model is not in trouble. The latest observations demonstrate that the more we learn about the origin, history, and structure of the universe and the more accurately we measure the characteristic features of the universe, the more evidence we accumulate for the supernatural design of the universe and for the big bang creation model.”
I think I’ll leave it there, as well.















