Jun
16
Part 2: Propositions and Logical Relationships
“Having, then, once introduced an element of inconsistency into his system, he was far too consistent not to be inconsistent consistently, and he lapsed ere long into an amiable indifferentism which to outward appearance differed but little from the indifferentism….” — Samuel Butler, iconoclastic Victorian author
Despite what you might think from the heading, this post has nothing to do with friends, dating, or marriage. Besides, we all know that logic goes out the door when it comes to that stuff…. 😉
In my initial post for this series, we examined the three founding principles of logic: the Law of Noncontradiction, the Law of Excluded Middle, and the Law of Identity. Now, we will look at the next level of basic principles necessary to get a handle on critical thinking — namely, the four types of logical relationships:
1) Contradictory
2) Contrary
3) Subcontrary
4) Subalternation
These build on the Three Laws, of course. But, in order to figure out when they apply, we also need to understand the four “categorical propositions”. (In the following, ‘A’, ‘E’, ‘I’, & ‘O’ are simply the standard way that the categorical propositions are abbreviated. I don’t know why. ‘S’ & ‘P’ represent what are called the subjective and predicate terms, respectively.):
Universal affirmative proposition – A: All ‘S’ are/do ‘P’.
Universal negative proposition – E: No ‘S’ are/do ‘P’.
Particular affirmative proposition – I: Some (at least one) ‘S’ are/do ‘P’.
Particular negative proposition – O: Some (at least one) ‘S’ are/do not ‘P’.
When statements that fit two or more of the categorical propositions are compared to each other, you can determine which of the four logical relationships is in play. This helps us understand how differing truth claims and positions relate to one another.
Got it? OK, here we go….
As you may have guessed, a contradictory relationship occurs when one (and only one) statement is true and one (and only one) statement is false. In other words, their claims contradict each other, or they “express opposite truth value”. Propositions ‘A’ & ‘O’ have a contradictory relationship; so do propositions ‘E’ & ‘I’.
For example, when commenting on the contents of my bookcase, if some books are blue, green, black, white, etc. — i.e., not red –, then I cannot also (with logical integrity) say that all the books are red. Makes sense, right? This is an example of the A/O contradictory relationship. An example of the E/I contradictory relationship is seen in these two statements:
E: “No Republicans are pro-choice.”
I: “Some Republicans are pro-choice.”
Obviously, if the latter is true — even if only one pro-choice Republican can be found –, this contradicts the claim of the former statement and makes it false.
A contrary relationship sounds a lot like a contradictory relationship, but the difference is important. The wording may sound awkward, but a contrary relationship means that not both statements are true. Or, put another way, they cannot both be true, but they may both be false. Propositions ‘A’ & ‘E’ have a contrary relationship. For example,
A: “All beings worshiped as (a) god/God exist.”
E: “No beings worshiped as (a) god/God exist.”
Pretty obvious that they can’t both be true, right? But, if we also consider the following,…
I: “Some (at least one) being(s) worshiped as (a) god/God exist(s).”
… we see that, if the ‘I’ statement is true, then the ‘A’ & ‘E’ statements are both false. The two universal statements are contrary. And, remember, the ‘E’ & ‘I’ statements are contradictory.
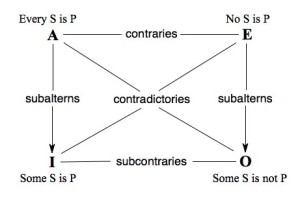The flip-side of the contrary relationship is the subcontrary relationship, which occurs when not both statements are false. In other words, they cannot both be false, but they may both be true. The two particular statements, ‘I’ & ‘O’, meet this criterion. So, for example,
I: “Some things in the biological realm can be explained by purely natural processes.”
O: “Some things in the biological realm cannot be explained by purely natural processes.”
Since the particular statements refer only to some of the subject meeting the predicate condition, then it is possible for both to represent objective truth. (I happen to think they do.) Yet, they cannot both be false, because they make opposite claims regarding the predicate.
Finally, we have subalternation relationships. Don’t let the strange word scare ya. What these relationships show is how a) truth in the universal statements guarantees truth in the corresponding particular statements (but not vice versa) and b) falsity in the particular statements guarantees falsity in the corresponding universal statements (but not vice versa). Suppose we know, for instance, that the following statement is true:
A: “All politicians are liars.”
It must also be true that:
I: “Some (at least one) politicians are liars.”
Both ‘A’ & ‘I’ are affirmative, or inclusive, statements. The “some” referenced in the particular statement is a subset of the “all” from the universal statement, which we have already established (or cynically assumed) to be true. But, if we start with the ‘I’ proposition as true, there is no guarantee that the ‘A’ proposition is true. Let’s look at another….
O: “Some humans are not sinful.”
If this particular statement is false, then the corresponding universal statement must also be false:
E: “No humans are sinful.”
False! Both ‘O’ & ‘E’ are negative, or exclusive, statements. Since the negative particular (particular negative?) proposition is not true, then its corresponding universal proposition must also be false.
Yeah, I know some of this stuff strains a few brain cells, but it really is necessary to review it before getting into the fun(ner) stuff. (If you’re having a little trouble, go back and re-read, mull it over and come up with examples of your own.) Stick with me, and you’ll be glad you did!
